그림들의 출처는 모두 EPFL의 MICRO-565, IEM NEUCHATEL PV-lab 에 있습니다
Prof. Christophe Ballif
PN 접합의 에너지 구조 그리기
diode하면 떠오르는 IV curve. IV curve의 모양새를 이해하기 위해 태양전지 pn 접합 내부에서 캐리어의 이동이 왜 일어나는지 이해해야 한다. Chap 8에서는 캐리어의 이동에 관한 수많은 공식을 배운다.
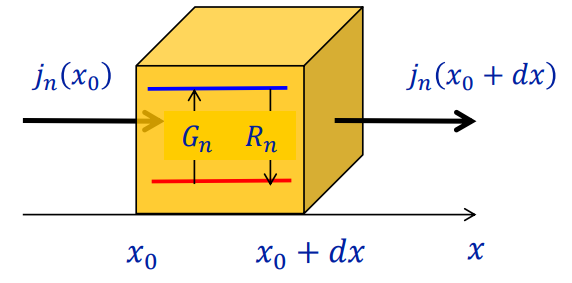
전류는 전하의 흐름이다. 위 그림에서 전류가 x0와 x0+dx 지점을 통과하고 있다. 두 지점을 지나면서 전류가 바뀌었다는 것은 흐르는 charge carrier의 수가 바뀌었다는 것이고, 이는 x0와 x0+dx 사이에서 캐리어의 농도가 바뀌는 원인이 된다. 특정 구간 x0 ~ x0+dx에서 시간에 따른 캐리어의 농도 변화를 나타낸 식을 continuity equation이라고 한다.
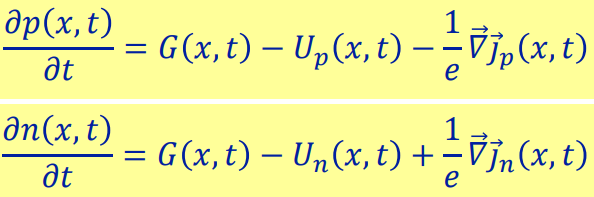
좌변은 단위 시간 당 홀 또는 전자 농도의 변화량이다. G는 생성 속도, U는 재결합 속도, ▽J는 전류 밀도의 변화이다. G는 캐리어를 생성하는 항이므로 + 부호이다. 재결합으로 인해 캐리어의 농도가 감소하므로 U 앞에는 - 가 붙는다. ▽J항을 이해하는 것은 조금 어려운데, 전류가 오른쪽으로 흐르려면 홀도 오른쪽으로 흘러야 하고 전자는 반대 방향 왼쪽으로 흘러야한다. 홀의 경우 전류 밀도가 커졌다는 것( ▽J>0)은 더 많은 홀이 오른쪽으로 빠져나갔다는 뜻이므로 홀의 농도가 줄어든다. 그래서 ▽J앞에 -가 붙는다. 반면 전자의 경우 전류 밀도가 커졌다는 것은( ▽J>0) 왼쪽으로 빠져나가는 전자보다 더 많은 홀이 오른쪽으로 들어왔다는 뜻이므로 전자의 농도가 증가한다. 그래서 ▽J앞에 +가 붙는다.
pn 접합에서 캐리어의 확산이 일어나는 구간을 space charge region(SCR), depletion region이라 한다.
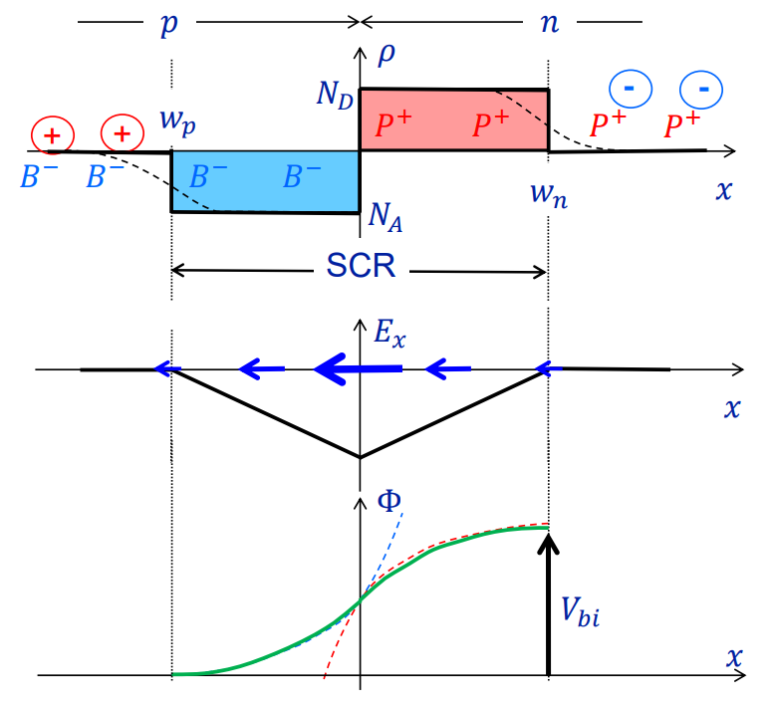
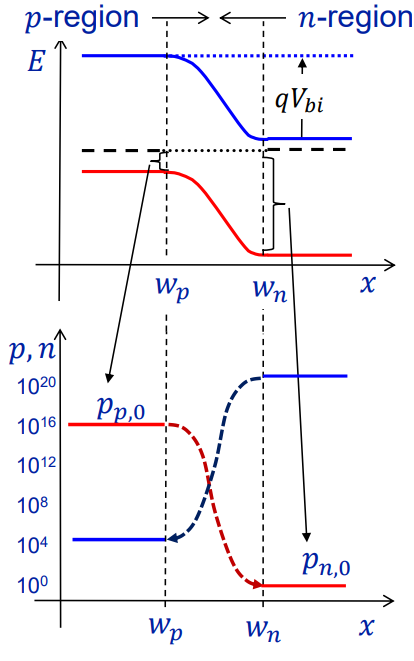
위에서부터 순서대로 전하 밀도, 전기장, 전위. wp는 SCR의 p형 반도체 쪽의 경계, wn는 SCR의 n형 반도체 쪽 경계.
전하 밀도: n형 반도체에서 풍부한 전자가 p형 반도체로 이동. interface부근에서는 전자가 부족해지면서 양전하를 띔. (빨간색 부분) p형 반도체에서 풍부한 홀이 n형 반도체 쪽으로 이동. interface 부근에서는 홀이 부족해지면서 음전하를 띔. (파란색 부분) 전하 균형이 항상 맞아야 하므로 파란 부분의 넓이와 빨간 부분의 넓이는 같아야 함.
전기장: 전기장은 +전하에서 -전하로 흐른다. 흐르는 방향이 -x 방향이므로 전기장은 음수이다. 전기장의 절댓값은 interface(x=0)에서 가장 크다. 이는 가장 확산이 잘 일어나 전하가 크기 때문이다.
전위: 전위는 전기장을 위치에 따라 음으로 적분한 것이다. 전기장이 음수이므로 전위는 오른쪽으로 갈수록 증가한다. +전하가 있는 곳이 높은 전위, - 전하가 있는 곳이 낮은 전위를 갖는다. wp의 전위를 0이라 두면 wn의 전위는 built in potential(V_bi)로 둘 수 있다.
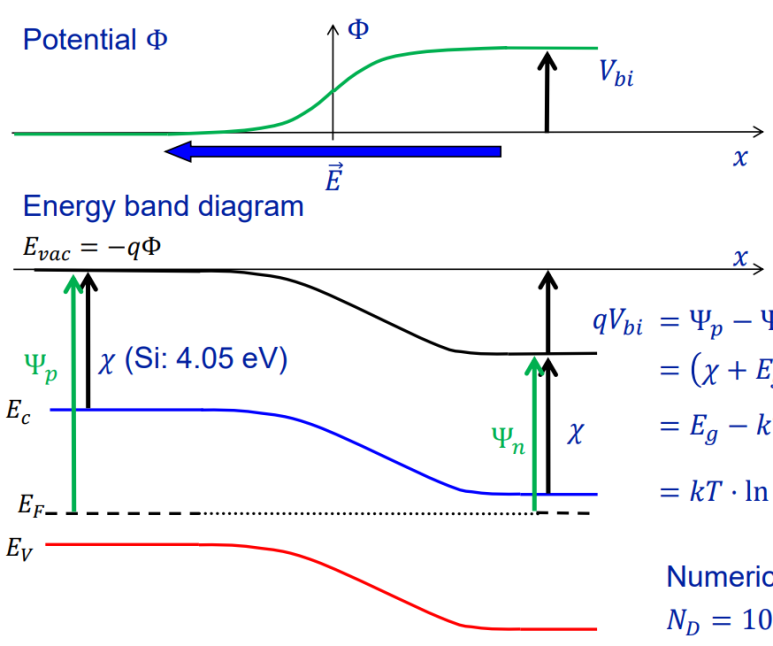
Ψ: work function, 전자를 고체로부터 떼어내는데 필요한 에너지
χ: electron affinity, 전자를 고체에 주입하는데 필요한 에너지
potential과 energy band는 반대 방향이다. potential은 단위 양전하(+1C)가 느끼는 에너지지만, energy band는 전자가 느끼는 에너지이기 때문이다. 전위가 높은 곳일수록 전자는 낮은 에너지를 가지고 안정해진다. 그래서 기울어지는 방향이 반대이다. energy band에서 built in potential은 p 반도체와 n 반도체 사이의 CB, VB 에너지의 차이이다. built in potential은 p형 반도체와 n형 반도체의 work function 차이로도 구할 수 있고, 기억할지 모르겠지만 ni^2 = N_c*N_v*exp(-E_g/kT) 식을 이용하면 다음과 같이 전개할 수 있다.
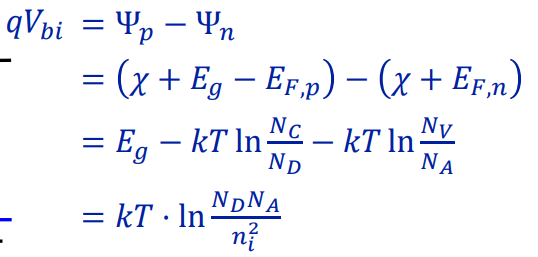
Bias에 따른 에너지 구조 변화
이를 통해 bias가 걸리지 않았을 때의 에너지 밴드를 다음과 같이 표현할 수 있다. 왼쪽이 p형 반도체, 오른쪽이 n형 반도체이다.
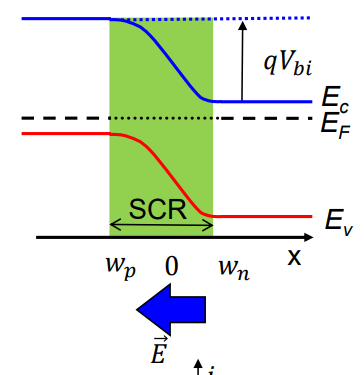
만약, p side에 음의 전압을 걸어준다면, p side의 에너지 밴드는 위로 올라간다. (전자는 음의 전압에서 높은 에너지를 가지고 양의 전압에서 낮은 에너지를 가지므로, 음의 전압을 걸면 전자의 에너지가 증가하는 위쪽으로 밴드가 올라간다.
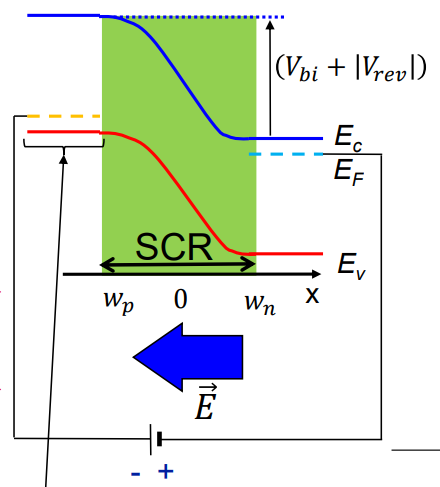
이 경우를 역방향 bias라 한다. SCR이 넓어지고 내부 전기장은 강해진다. 그리고 built in potential은 증가한다. 반대로 p side에 양의 전압을 걸면 에너지 밴드는 낮아진다. SCR은 줄어들고 built in potential도 감소한다. 내부 전기장도 약해진다. 이 경우를 정방향 bias라고 한다.
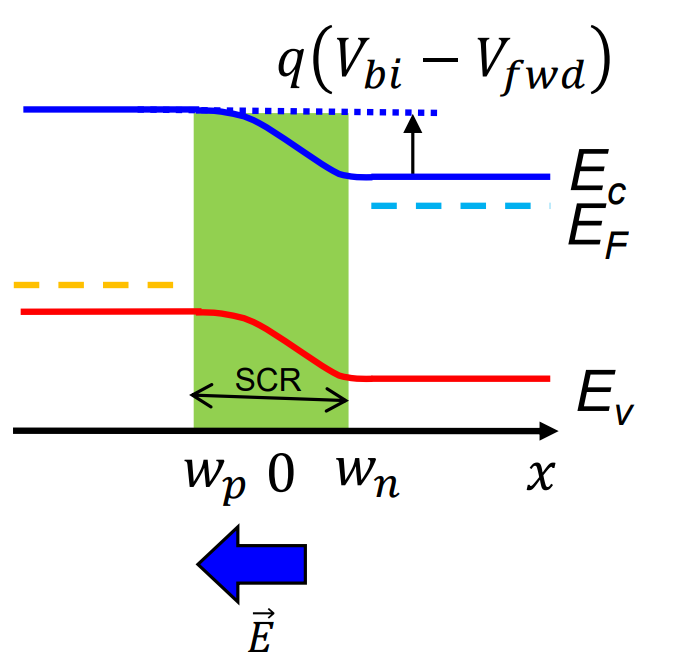
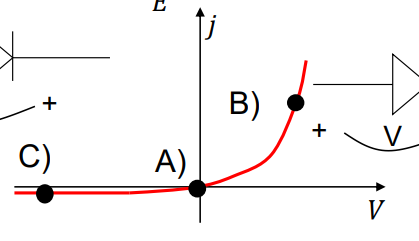
위 그림은 빛이 없을 때 dark condition의 I-V curve이다. bias가 없는 A에서는 전류가 흐르지 않는다.
역방향 bias C)에서는 n형 반도체에서 p형 반도체쪽으로 전류가 흐른다. (강한 전기장에 의해 전자가 p형 반도체에서 n형 반도체로 이동한다) 따라서 역방향의 전류가 흐르게 된다. 다만, p형 반도체 자체에 전자가 별로 없기 때문에 전류가 많이 흐르지 못한다. 반대로 정방향 bias B)에서는 p형 반도체에서 n형 반도체로 전류가 흐른다. 이는 낮아진 장벽으로 인해 n형 반도체의 풍부한 전자가 p형 반도체로 쉽게 이동할 수 있기 때문이다. 홀의 경우도 마찬가지이다. 캐리어의 농도가 높기 때문에 많은 양의 전류가 흐를 수 있다.
PN접합 내부에서 캐리어 농도
이제 pn 접합 내부의 캐리어 농도를 구해볼 것이다. p형 반도체에서 홀의 농도는 acceptor의 농도와 같다.
p(p,0) = N_A
n형 반도체에서 홀의 농도는 donor의 농도에 반비례한다.
p(n,0) = n(i)^2/N_D
아까 위에서 봤었던 공식을 조금 변형하면 다음과 같다.
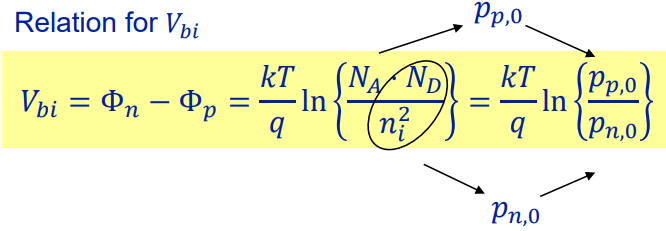
즉, built in voltage만으로 p형 반도체와 n형 반도체 내부의 홀의 농도비를 알아낼 수 있다. 전자 역시 똑같이 적용된다.

V(bi)는 양수이다. 이를 고려하면 p(n,0) < p(p,0)이고 n(n,0) > n(p,0)이다.
p(n,0) : n형 반도체에 들어있는 홀 농도
p(p,0) : p형 반도체에 들어있는 홀 농도
n(n,0) : n형 반도체에 들어있는 전자 농도
n(p,0) : p형 반도체에 들어있는 전자 농도
임을 생각했을 때 당연한 소리이다.
이 농도는 SCR 범위 밖에서의 캐리어 농도이고, SCR 내부의 농도를 정확히 아는 것은 어렵다.
이제는 forward bias가 걸렸을 때 홀과 전자의 농도에 어떤 변화가 생기는지 알아보자. 몇 가지 가정이 필요하다. p형 반도체에서는 이미 홀이 풍부하기 때문에 전압이 걸린다고 농도가 그렇게 크게 바뀌지 않는다. 따라서, p(p,0)는 바뀌지 않는 것으로 할 것이다. 반면, n형 반도체에서는 홀이 부족하기 때문에 전압이 걸리면 농도 변화량이 크다. 따라서, p(n,0)는 p(n)으로 바뀐다. SCR의 경계를 wp, wn이라고 하면
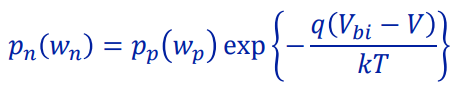
이다. 이 때, p_p(wp) = p(p,0)이고

임을 기억하면
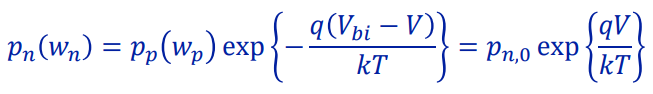
로 확장할 수 있다. 따라서 bias가 없을 때 n형 반도체에서 홀의 농도와 bias가 있을 때 n형 반도체의 wn 위치에서 홀의 농도 사이에는 forward bias로 걸린 전압에 exponential한 관계가 생긴다. wn 위치에서 홀의 농도를 구한 이유는 SCR과 n-region의 경계이기 때문이다. wn보다 오른쪽 구간에서는 농도를 예측할 수 없다.
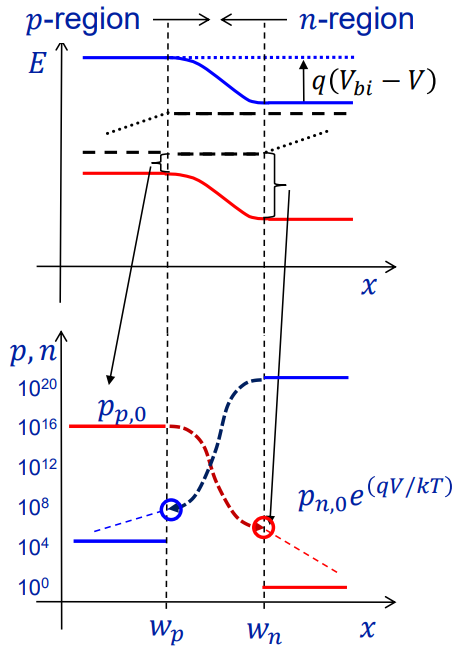
홀: 홀은 p side에서 많고 n side로 갈수록 적어진다. 하지만, wn위치에서 홀의 농도는 forward bias로 인해 bias가 없을 때보다 exponential하게 증가했다. wn보다 오른쪽으로 가면 홀의 농도가 계속 줄어든다. 만약, +∞까지 갔다면 그 때는 bias가 없을 때 p(n,0)과 같게 될 것이다.
이는 전자에 대해서도 똑같이 적용된다. 전자의 경우 n_n(wn) = n(n,0)이고,
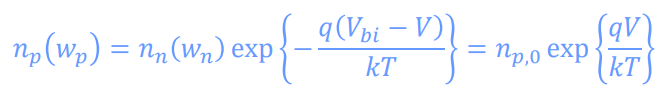
bias가 없을 때 p형 반도체에서 전자의 농도와 bias가 있을 때 p형 반도체의 wp 위치에서 전자의 농도 사이에는 forward bias로 걸린 전압에 exponential한 관계가 생긴다.
SCR 밖에서의 캐리어 농도 변화
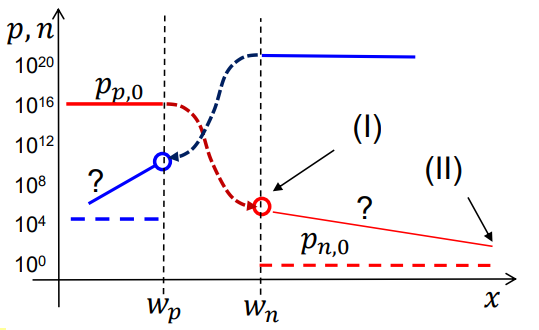
이제는 wn, wp 경계에서의 농도가 아닌 그 밖을 넘어섰을 때 농도 변화를 확인하자. 특정 위치에서 시간에 따른 홀의 농도 변화는 (생성되는 양 - 사라지는 양 - 다른 곳으로 이동하는 양)
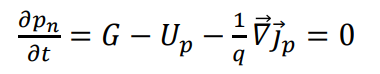
dark condition이므로 G=0이다.
정류 상태(시간에 따라 농도가 변하지 않음)를 가정하면
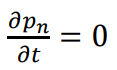
이다.
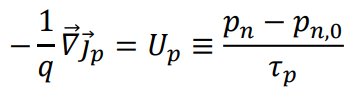
이는 어떤 두 공간에서 측정한 전류 밀도의 차이는 그 만큼의 해당하는 홀의 재결합 과정으로 인해 발생한다는 것이다. 홀의 재결합으로 인해 홀의 농도가 감소하고 이는 두 공간 상에서 전류밀도의 차이를 만든다.
SCR 외부에서는 전기장이 없기 때문에 전기장에 의한 전류가 없고 오직 확산에 의한 확산 전류만 존재한다.
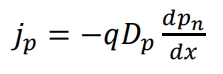
이 전류가 SCR에서의 전류가 되는 것이므로 위 두 식을 연결하면
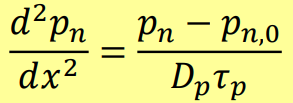
이고, 이차 미분 방정식을 풀면
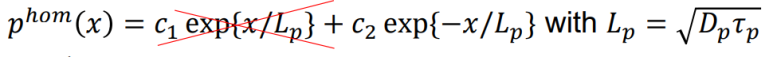
이 된다. 첫 번째 항은 지워져야 하는데, 그 이유는 x가 +∞가 될 때 홀의 농도가 수렴해야지, 발산하면 안 되기 때문이다. 따라서 c1 = 0으로 둔다. 경계 조건에는 두 가지가 있다. 1) wn에서의 홀의 농도는 원래 홀의 농도에 forward bias 전압 V로 인한 exp 항을 곱해서 구한다. (아까 봤던 식) 2) +∞에서는 원래 홀의 농도와 같아진다.
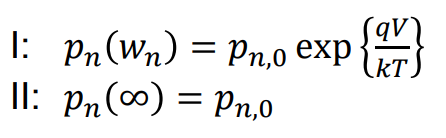
두 경계 조건을 이용해
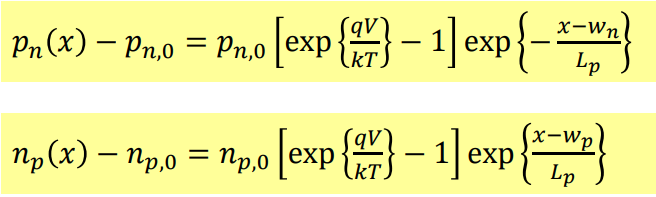
이렇게 홀의 농도, 전자의 농도가 SCR밖에서 지수함수의 관계를 가짐을 알 수 있었다.
PN접합에서의 carrier current
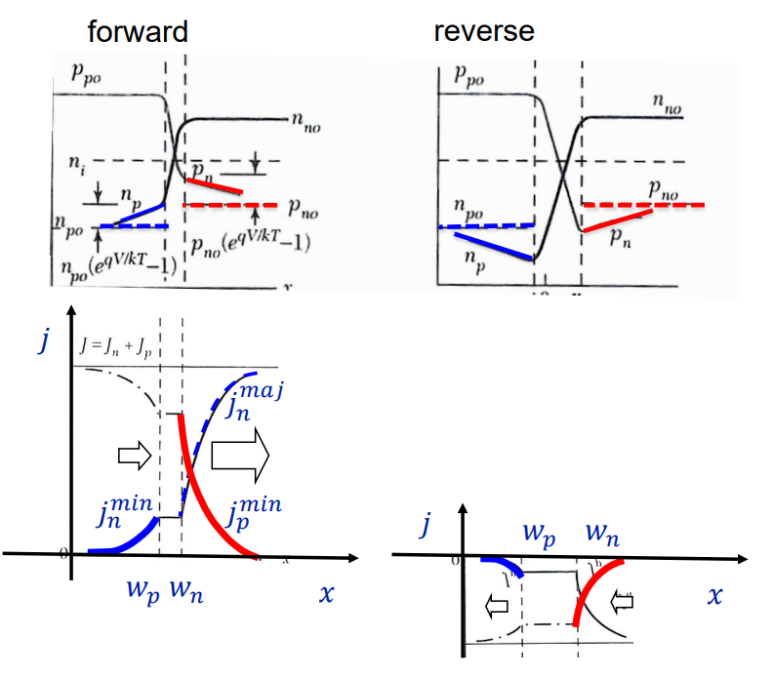
forward bias가 걸리면 n형 반도체 내부의 홀의 농도는 증가하고 p형 반도체 쪽의 전자 농도도 증가한다. minority 캐리어의 전류가 증가하면서 전체적인 전류 밀도가 증가한다. 하지만 접합에서 구간에 따른 전체 전류 밀도는 일정하다. reverse bias에서는 n형 반도체 내부의 홀의 농도는 감소하고 p형 반도체 쪽의 전자 농도도 감소한다. minority 캐리어의 전류가 감소하면서 전체적인 전류 밀도가 감소한다.
n-side에서 홀의 농도는 다음과 같이 쓸 수 있다.
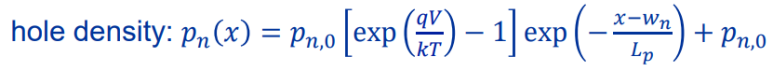
홀에 의해 발생하는 current는 확산에 의한 것이므로
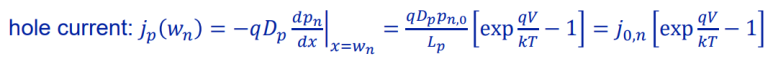
로 쓸 수 있다. 이 때, 초기값 역할을 하는 j(0,n)은 n-side에서의 saturation current density가 된다.
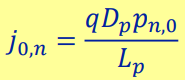
위 식을 p-side에서의 전자에도 적용할 수 있다.
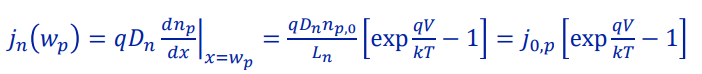
따라서, total current density는 홀에 의한 전류와 전자에 의한 전류의 합이므로
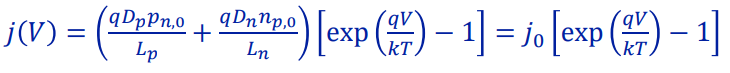
이라는 간단한 식으로 정리할 수 있다. 이 때, j0는
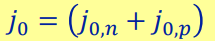
이다. 이 식이 dark condition의 IV curve가 된다.
'태양전지 교과서' 카테고리의 다른 글
| [태양전지 교과서] Week 8 - Finite Solar Cell (0) | 2025.01.26 |
|---|---|
| [태양전지 교과서] Week 8 - Photocurrent in illuminated p-n solar cell (0) | 2025.01.26 |
| [태양전지 교과서] Week 7 - Recombination process (0) | 2025.01.26 |
| [태양전지 교과서] Week 7 - Generation & Recombination (0) | 2025.01.26 |
| [태양전지 교과서] Week 6 - Direct and Indirect Bandgap (0) | 2025.01.26 |



