[태양전지 교과서] Week 7 - Recombination process
그림들의 출처는 모두 EPFL의 MICRO-565, IEM NEUCHATEL PV-lab 에 있습니다
Prof. Christophe Ballif
앞서 recombination은 전자와 홀이 만나 pair가 소멸되는 것이라고 했다. recombination 종류에도 여러 가지가 있다.
1. Radiative recombination
2. Auger recombination
3. Shockley-Read-Hall recombination
4. Surface recombination
Radiative recombination
가장 기본적인 재결합 과정. 'absorption'의 반대 과정이다. 빛을 받으면 전자가 에너지를 얻어 전이하고 들뜬 전자와 양공이 생기듯이, 반대로 들뜬 전자와 양공이 재결합해 빛 등의 에너지를 방출한다. direct 반도체의 경우 radiative recombination은 빠르지만, indirect의 경우 느리다. direct bandgap에서 전자의 전이는 2 particle interaction(전자와 photon)이지만, indirect bandgap에서는 3 particle(전자 + photon + phonon)이기 때문에 훨씬 어렵고 느리게 일어난다. radiative recombination은 전자와 양공이 하나씩 필요하므로 이 둘의 농도가 증가할수록 빠르게 일어난다.
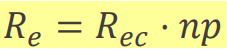
R_e는 재결합 속도, R_ec는 상수
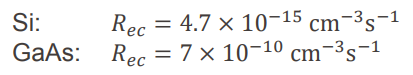
GaAs는 direct bandgap, Si는 indirect라 그런지 R_ec는 GaAs가 훨씬 크다.
dark condition에서는 빛이 없으므로 전자와 홀의 농도는 초기 농도와 같고 재결합 속도는
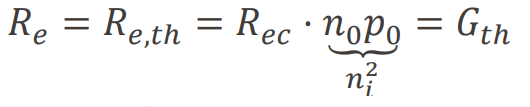
로 표현된다. dark condition에서는 재결합 속도와 thermally 생성되는 캐리어가 균형을 이루므로 이는 G_th와 같다. 만약, 빛이 주어지는 illumination 환경이라면, illumination에 의해 발생하는 재결합 속도는
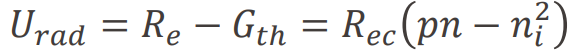
이는 illumination에 의한 재결합 = 전체 재결합 - 열에 의한 재결합 이기 때문이다.
그럼 이제 low injection과 high injection 경우에 캐리어의 수명을 확인할 건데, 여기서 low injection은 광 조사가 그렇게 강하지 않아 반도체 내부의 majority 캐리어 농도에만 별 변화가 없지만, minority 캐리어는 많이 바뀌는 경우이다. 예를 들어,
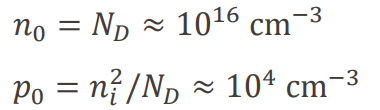
위 조건의 n-type 반도체가 있다고 가정했을 때,
빛에 의해 전자와 홀 모두 10^14 만큼 증가한다고 가정하면
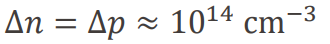
전자 농도는 사실 그렇게 변하지 않지만(10^16+10^14 ≒ 10^16) 홀의 농도는 매우 변한다. (10^4 + 10^14 ≒ 10^14) 이 경우 illumination에 의한 재결합 속도는 U=R_ec * n * p 대신에
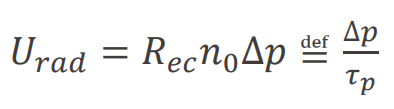
로 쓸 수 있고,
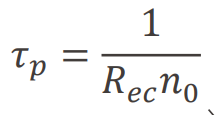
캐리어의 수명은 상수 형태로, 빛의 세기와 무관하다.
반면 high injection은 빛이 강해서 majority carrier랑 minority carrier의 농도가 모두 바뀌는 경우이다. 이러면 빛에 의해 생기는 전자와 홀의 농도가 중요해진다.

그러면 재결합 속도 U = R_ec * n * p는
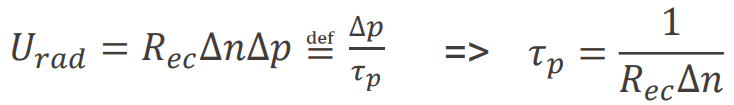
위처럼 쓸 수 있고, 캐리어의 수명은 injection level에 의존하게 된다.
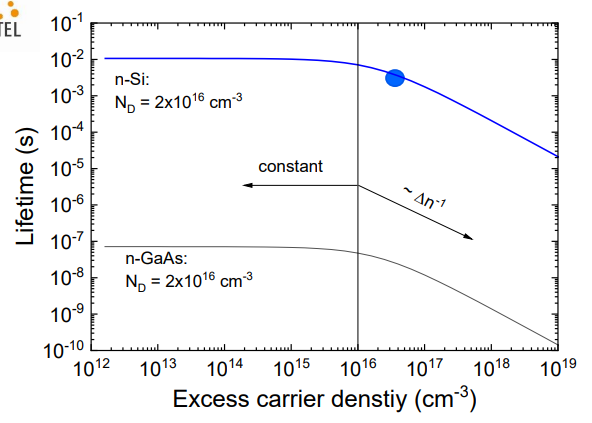
빛이 약해 carrier가 잘 생기지 않는 왼쪽 영역은 수명이 일정하지만, 빛이 강해 carrier가 많이 생기는 오른쪽은 빛의 세기에 따라 lifetime이 변한다. 수명은 △n에 반비례한다.
Auger recombination
조금 더 복잡한 재결합 과정이다.
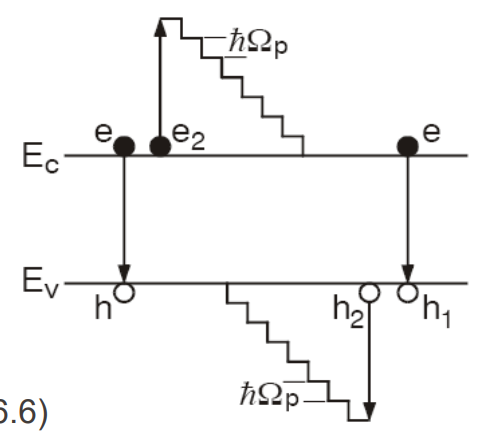
재결합 과정에서 방출된 에너지가 빛의 형태(photon)로 방출되지 않고 다른 전자로 전달되는 재결합.
위 그림에서 전자 e과 홀 h와 재결합할 때 방출된 에너지는 전자 e2가 흡수하여 더 높은 에너지로 전이하는데 기여한다. 그 뒤, 들뜬 전자 e2는 phonon scattering을 통해 다시 안정화된다.
이 상호작용은 3 particle interaction이다. 전자와 홀, 그리고 또 다른 전자가 필요하거나 또 다른 홀이 필요하다. 즉 전자 2개와 홀 1개 또는 전자 1개와 홀 2개가 필요하다.
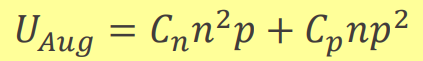
방금 했던 것처럼 똑같이 low injection과 high injection 과정을 나눠서 생각하면,
n-type 반도체에서 low injection에서는 전자의 농도는 똑같고, 홀의 농도만 빛에 의해 변하므로

이므로,
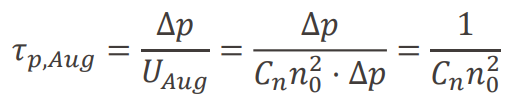
수명이 일정한 상수로 나타난다.
high injection에서는
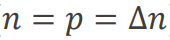
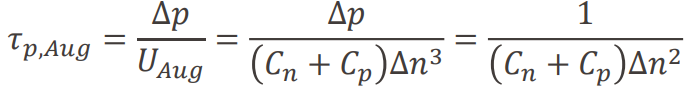
이므로 수명이 △n^2에 반비례함을 알 수 있다.
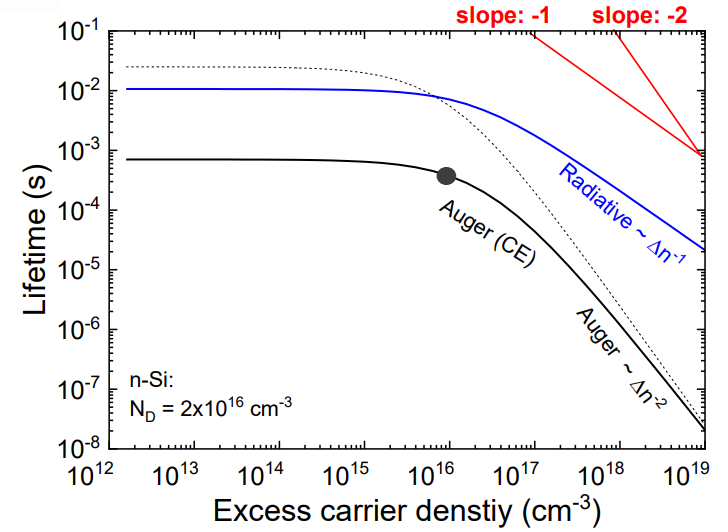
그래서 같은 그래프 위에 radiative와 auger recombination에 의한 lifetime을 각각 표기하면 auger 선의 경우 기울기가 더 가파르다.
Shockley-Read-Hall recombination(SRH)
태양전지에서 가장 중요한 recombination 과정으로, 반도체에 도핑한 dopant의 에너지 준위에 의해 발생한다.
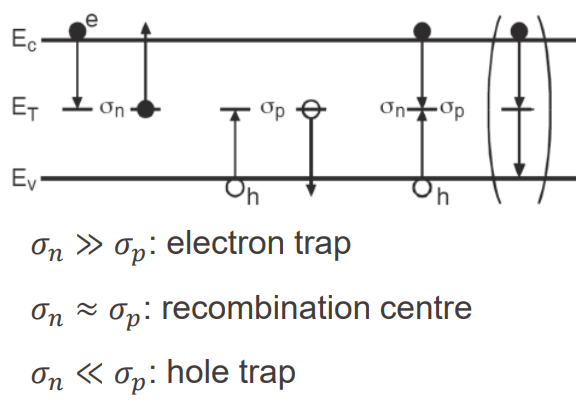
원래 dopant는 반도체에 캐리어를 공급해주는 역할을 했으나, 비어있는 dopant는 반대로 캐리어를 잡아두는 trap의 역할도 할 수 있다. 이 때, σ_n, σ_p를 capture cross section이라고 하는데, 각 dopant가 캐리어를 잡아두는 능력을 나타낸 값이다. electron trap은 전자를 잡아둔다. 물론, trap에 잡힌 전자가 다시 CB로 올라갈 수 있다. hole trap은 홀을 잡아둔다. 물론, trap에 잡힌 홀은 다시 VB로 전이할 수 있다. 때문에 trap 자체는 태양전지 효율에 그렇게 악영향을 미치지 않는다. 하지만 recombination center은 전자와 홀을 모두 잡아두면서 재결합의 중심지로 작동한다. 이는 태양전지 내부의 캐리어 농도를 줄이면서 효율을 감소시킨다.
Shockley-Read-Hall recombination의 속도식은 어떻게 계산한 건지는 모르지만.
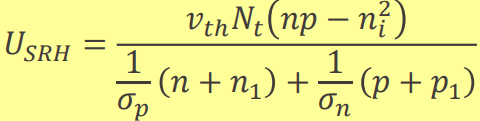
이다. N_t는 defect(trap)의 농도이다. N_t와 σ가 클수록 재결합이 빨라진다.
계산을 쉽게 하기 위해 여러 가지 가정을 하고 위 식을 정리하면,
1) low injection인데 σ_n = σ_p 이고 trap이 bandgap의 중앙에 위치할 경우(E_t = E_i)
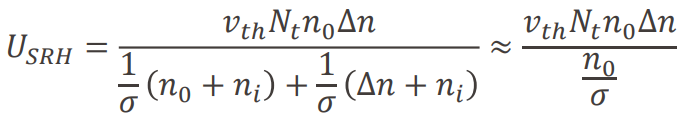
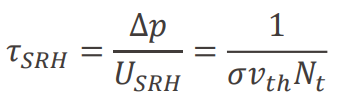
캐리어의 수명이 △n에 의존하지 않는 상수이다.
2) low injection인데 trap이 bandgap의 중앙이 아닐 때, (E_t ≠ E_i)
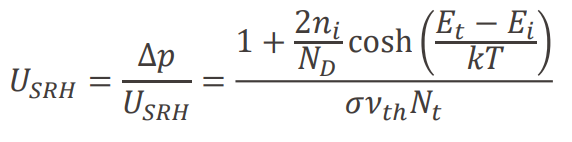
cosh이라는 복잡한 식이 나온다. (위에 △p/U_SRH는 △p/τ로 바꿔야할 듯..) 때문에, 캐리어의 수명을 한 눈에 파악하기 위해 그림으로 그리면
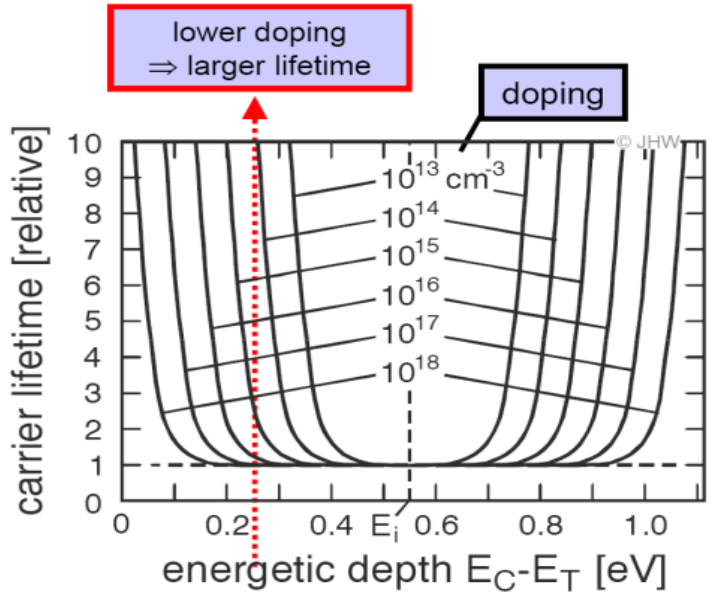
으로 나온다. doping level에 관계없이 trap의 에너지 준위가 bandgap 중앙일 때 carrier의 수명이 제일 짧아서 안 좋은 case이다. 그리고 doping level이 증가할수록 수명이 짧은 구간이 증가하면서 안 좋은 영향을 미친다. 즉, 높은 농도의 dopant는 mid gap에서 멀리 떨어진 defect trap도 활성화시키면서 재결합을 활성화시킨다. 태양전지에 안 좋다. 무작정 doping을 강하게 한다고 좋은 게 아니다.
3) high injection의 경우

로 정의하면
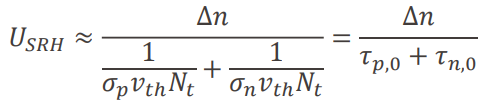
가 되어 캐리어의 수명이 다음과 같이 표현된다.
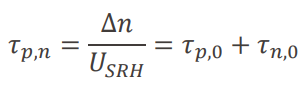
일정한 값이지만, 값 자체는 low injection일 때와 다르다.
지금까지 배운 모든 recombination을 하나의 그래프 위에 표시하면
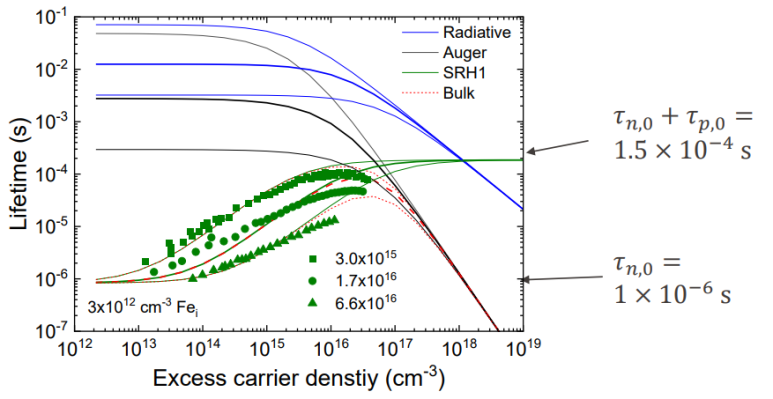
ex. 위 그래프는 FeB complex의 그래프로, p-type 태양전지의 주요 불순물로 꼽힌다. trap의 에너지는 mid gap과 가깝다.
여기서 알 수 있는 포인트
- recombination이 radiative, auger, SRH 3가지로 이뤄짐
- 빨간 선은 캐리어의 최종 수명이다. 주로 수명이 가장 낮은 recombination에 의해 결정됨.
- 파란선(radiative)는 주로 위에 있어서 carrier의 수명을 제한하는데 별로 기여하지 않음
- carrier가 적을 때는(왼쪽, low injection) 초록선이 캐리어의 수명을 결정. 즉, SRH가 주로 기여
- carrier가 많을 때는(오른쪽, high injection) 검정선이 캐리어의 수명을 결정. 즉, auger process가 주로 기여.
- 이를 통해 전자와 홀의 수명을 각각 알 수 있음. 초록선의 왼쪽 절편은 전자의 수명, 초록선의 오른쪽 절편은 전자와 홀의 수명의 합.
다른 유형의 그래프도 있다.
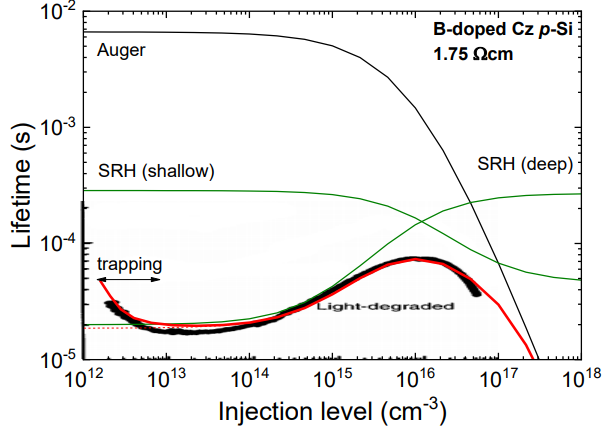
위 그래프는 BO complex의 그래프이다. BO는 태양전지의 실리콘 웨이퍼를 만드는 공정에서 생기는 불순물이다.
FeB와 달리 BO에는 두 가지의 defect가 있다. 하나는 shallow defect로 trap 에너지의 위치가 VB에 가깝다. 하나는 deep defect로 trap 에너지 위치가 mid gap에 가깝다. 그 결과 SRH 선이 두 가지로 나타난다.
여러 가지의 recombination으로 인해 나타나는 최종적인 수명은 어떻게 구할까?
최종 수명 = radiative 수명 + auger 수명 + SRH 수명
이런 식이 아니다. 왜냐하면 각각의 재결합 과정은 캐리어의 수명을 방해하는 요인이기 때문에, 수명이 줄었음 줄었지 저런 식으로 더하진 않는다.
그래서 최종 수명은 각각의 수명을 역수 취급하여 더한다.
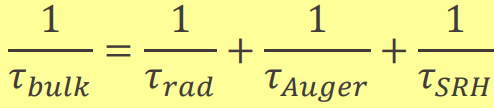
이렇게 계산된 수명은 bulk 수준에서의 캐리어 수명이다. 표면에서 무슨 일이 일어나는지 고려하지 않았기 때문이다.
Surface recombination
마지막 재결합 과정은 surface recombination이다. 표면에서 일어나는 재결합으로, bulk 수준의 물질과는 달리 표면은 원자들의 구성과 배열 등이 다르기 때문에 또 다른 trap이 만들어진다.
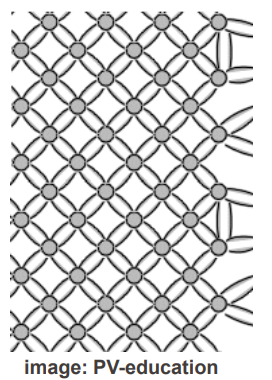
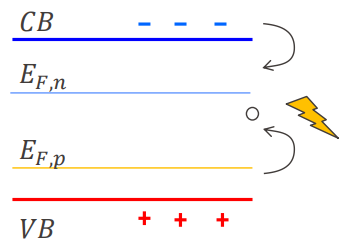
표면에 있는 원자들의 결합에는 문제가 많으므로 defect가 생기기 쉽고 위 그림의 하얀 점과 같이 defect로 인한 에너지 trap이 생긴다. surface recombination의 속도는 다음과 같이 표현할 수 있다.
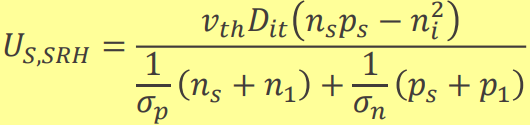
SRH recombination과 형태가 비슷해보인다. 식이 복잡한데, 굳이 식이 어떻게 생겼는지 알 필요는 없다. 원래 이런 건 외우는 게 아니라 나중에 필요할 때 써먹으려고 이런 게 있구나를 미리 알아두는 거다. 근데 나는 별로 필요 없을 것 같다. 그래도 저런 식이 '존재한다' 자체를 아는 건 나중에 도움이 될 수도 있다. D_it는 surface state density이다. 단위는 /cm².
n-type 반도체, low injection, midgap defect임을 가정하면 위 식을 간단히 만들 수 있다.
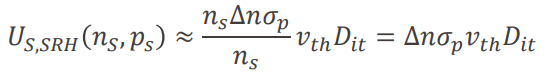
여기서 새로운 개념을 정의할 수 있다.
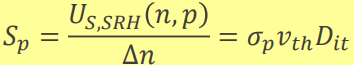
surface recombination velocity라고 실제 velocity가 아니라 (나는 왜 만들었는지 모르겠는) parameter이다. 그 정의 방식이 lifetime과 비슷하다.
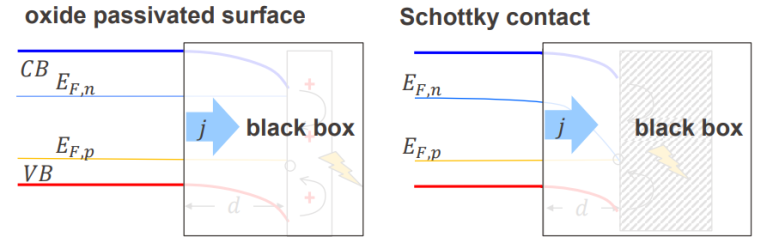
surface recombination을 bulk recombination과 같이 계산하려면 위 처럼 band를 평평히 한다고 가정해야한다. 원래 표면에서는 band가 휘어진다. 휘어지는 이유는 interface사이에서 발생하는 캐리어의 확산과 전기장 때문인데 자세한 건 반도체나 광화학 수업에서 다룬다. 아무튼, 표면에서의 재결합은 진짜 표면이 아닌 depletion region의 끝자락에서 effective surface recombination velocity를 써서 다시 쓸 수 있고,
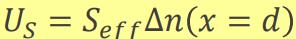
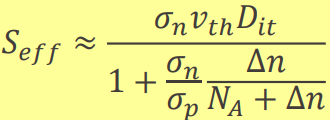
위와 같이 표현된다.
따라서, 전체적인 수명은 bulk와 surface를 모두 고려한
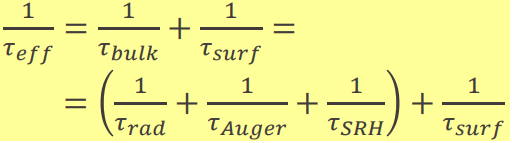
로 표현된다. 유난히 힘들었던 chap 7이었다.