[태양전지 교과서] Week 5 - Fermi level & Fermi-Dirac distribution

그림들의 출처는 모두 EPFL의 MICRO-565, IEM NEUCHATEL PV-lab 에 있습니다

Prof. Christophe Ballif

페르미 준위: T=0K일 때는 전자가 존재할 수 있는 가장 높은 에너지 레벨, T>0K일 때는 전자의 발견 확률이 50%인 곳.

주의할 점은 전자가 절반 채워져있다는 게 아니다. 그냥 이론적으로 계산을 해봤더니 여기에 전자가 존재할 확률이 50%라는 것이다. 실제로 fermi level은 주로 밴드갭에 위치해있다. 알다시피 밴드갭에서는 전자가 존재할 수 없다. 실제로 전자가 존재할 수 없는 곳이지만, 만약 전자가 존재했다면 50% 차있었을 거라는 뜻이다.

​

전자는 에너지가 낮은 곳에는 많이 모여있고 높은 곳에는 적다. 과학자들은 에너지에 따른 전자들의 분포를 알기 위해 fermi-Dirac distribution이라는 식을 찾아내었다.

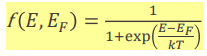
그래서 전자가 존재할 확률 f는 에너지(E), 온도(T) 등에 의해 달라진다.

​

T>0K일 때, 전자의 에너지가 fermi level(E_F)이면 (E=E_F), f = 0.5가 된다. 즉, 전자가 존재할 확률이 50%가 된다. 실제로는 전자가 존재하지 않는다. 왜냐면 밴드갭에 위치해 있기 때문에 전자가 들어갈 수 있는 자리 자체가 없다. 하지만, 만약 자리가 있었다면 50% 차있었을 것이다.

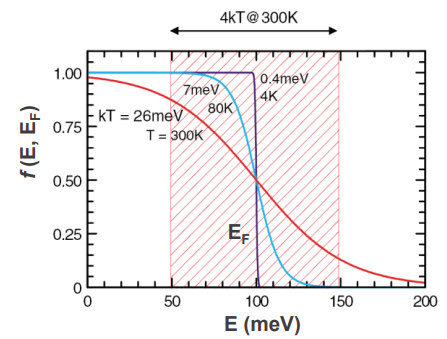
온도에 따라 곡선의 모양이 달라진다. 절대영도일 경우 직사각형 모양이다. 어느 한 순간에 전자가 존재할 확률이 1에서 0으로 떨어진다. 그래서 페르미 준위의 정의가 전자가 존재할 수 있는 최대 에너지 레벨이 되는 것이다. 온도가 T>0K일 경우, 항상 fermi level일 때 f=0.5이다. 따라서, 정의가 그렇다. 온도가 높아질수록 VB에 있었던 전자가 CB로 올라간다. 그래서 온도가 높아질수록 VB쪽(낮은 에너지)의 f는 줄어들고 CB(높은 에너지)의 f는 증가한다. 

​

자유전자는 E_c 이상의 에너지를 갖는 전자들이다. 즉, CB에 있는 전자들만 자유전자로 생각하므로, 자유전자의 개수를 구하기 위해선 CB에 들어있는 전자 수를 구하면 된다.

​

CB에 들어있는 전자 수는 어떻게 구할까? 각 에너지 level별로 존재하는 전자 개수를 모두 더하면 된다. CB에서 가장 낮은 에너지 레벨은 E_c이므로 E_c부터 ∞까지 전자 개수를 적분하면 된다. 그래서 전자 개수는 (각 에너지 레벨에서의 가능한 전자 자릿 수, g) X (전자가 자리를 채울 확률, f)를 CB의 에너지 범위(E_c ~ ∞)로 적분하면 된다.

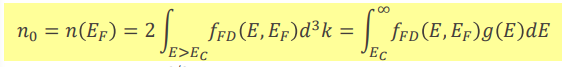
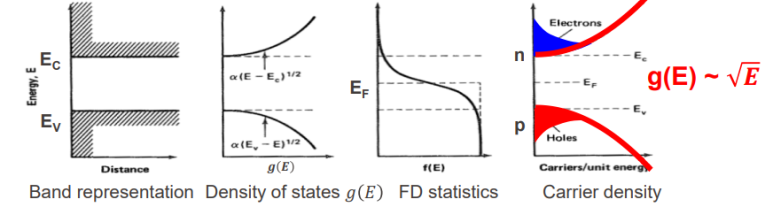
그래서 위와 같다. g는 density of state(전자가 들어갈 수 있는 자리), f는 전자가 자리를 채울 확률, 마지막 그림이 실제 전자와 홀 개수의 분포이다. 어렵다고 느껴질 수 있는데 나도 처음에는 하나도 이해가 되지 않았다. 혹시라도 어렵다면 댓글로 알려주세요...

​

저렇게 자유전자, 홀의 개수를 잘 정리해서 표현하면

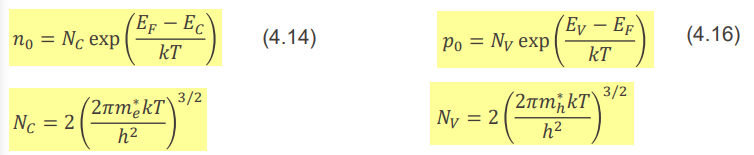
위와 같은 공식으로 표현할 수 있다. n0, p0가 자유전자, 자유홀의 밀도이다. 이 때, N_c는 전자가 들어갈 수 있는 전체 자리의 밀도, N_v는 홀이 들어갈 수 있는 전체 자리의 밀도(자리의 밀도란? 단위 부피 안에 자리가 몇 개 있는지를 말한다고 생각하면 된다)라고 생각하면 된다. 아무것도 첨가되지 않은 intrinsic SC의 경우, n0=p0여야 한다. 왜냐하면, 전자가 위로 올라간 만큼 valence band에 홀이 생길 것이기 때문이다. 따라서, n0=p0라 두고 fermi level을 계산할 수 있다.

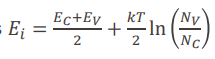
또한, n0=p0이므로 n0 X p0 = n0²이다. 이를 표현하면

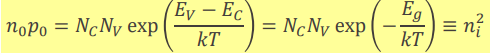
N_c, N_v, E_g는 모두 상수이므로 온도만 일정하면 n0*p0값은 언제나 일정하다.

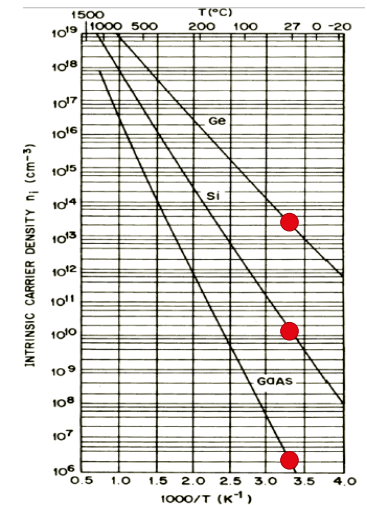
실제로 온도가 증가할수록(왼쪽) 밴드갭이 작을수록(Ge<Si<GaAs) 캐리어 농도가 커진다.