그림들의 출처는 모두 EPFL의 MICRO-565, IEM NEUCHATEL PV-lab 에 있습니다
Prof. Christophe Ballif
지금까지는 태양전지가 발전되고 우리 생활에 끼치는 macroscopic 면을 봤지만, 이제부터는 태양전지 속의 microscopic한 면을 볼 것이다. 태양전지의 가장 중요한 특징은 p-n 접합이다. p-n접합을 이해하기 위해선 doping에 대해서 이야기해야한다. 그리고 doping을 알기 위해선 에너지 밴드부터 알아야 한다.
전자는 입자로만 보면 안 된다. 우리는 전자를 파동으로 볼 필요가 있다. 전자가 파동의 성질을 가질 때, 우리는 전자를 파동 함수로 나타낼 수 있다. (파동이니깐) 이 파동 함수의 파장에 따라 전자의 momentum, k가 달라지고, 이 k가 전자의 E를 결정한다.
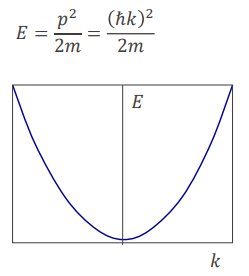
free electron model
전자가 자유로울 때(외부 potential의 영향을 받지 않아 자유롭게 이동할 수 있을 때), free electron model을 적용할 수 있다. 전자의 움직임이 자유롭기 때문에 전자는 모든 k값을 가질 수 있다. 이 경우의 조건을 free electron이라 한다.
하지만, 전자가 어떤 상자, 구역 안에 갇혀있고 그로 인해 전자의 움직임이 제한될 경우, 전자가 가질 수 있는 k도 제한된다. 이는 전자가 움직이는 제한된 구역 안에서 정상파 모양을 이루며 움직여야 하기 때문에 이런 조건이 발생한다.
정상파가 만들어지는 조건은 전자의 momentum(k)과 상자의 길이 (L)를 곱한 것이 2pi의 정수배여야 한다.
κ×L=2nπ

정상파는 양끝에서 파동의 위상이 0이어야 한다. 즉, box의 길이가 L이고, 전자의 파동함수를 y=sin(kx)라 할 때 x=L 일 때의 위상이 0이어야 한다는 뜻이다. sin(kL) = 0 이려면, kL = 2nπ 여야 한다. (전자 파동함수를 y=sin(kx) 이라 한 것은 주기함수 꼴로 표현해야 하니깐 주기함수 중 가장 대표적인 sin 함수를 가져왔다고 생각하면 편하다.)
즉 전자의 momentum, k값은 2nπ/L로 제한된다. 그래서 한정된 E만을 가질 수 있게 된다. 이 조건을 particle in a box라 한다.
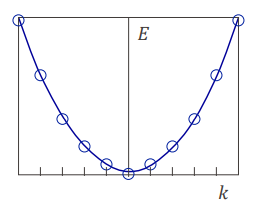
Particle in a box
만약, 전자가 하나의 상자가 아니라 여러 개의 원자 속에 갇혀있다면 어떻게 될까? 이 조건은 periodic potential이라고 한다. 말 그대로, 전자의 움직임을 제한하는 상자(원자)가 한 개가 아니라 주기적으로 배치되어 있어 전자의 움직임이 주기적으로 변하는 조건이다.
고체 속에서 원자가 주기적으로 배열되어 있기 때문에 전자 역시 원자들로부터 주기적인 상호작용(인력)을 받는다. 똑같은 주기로 원자가 배열되어 있기 때문에 원자로부터 받는 힘도 주기적인 것이다. 이 주기적인 인력으로 인해 전자의 파동함수가 주기적으로 영향을 받고, 전자의 에너지는 주기함수로 표현된다.
Periodic potential(까만 점: 원자핵 위치)
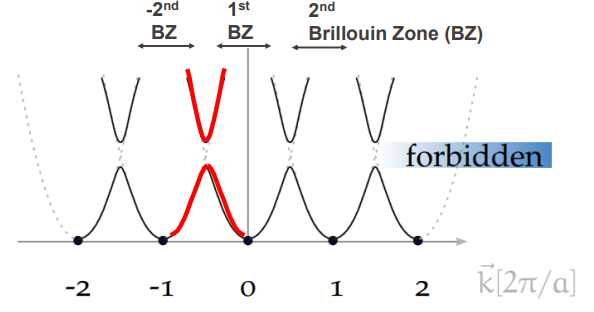
위 그림이 바로 periodic potential에서의 전자의 E-k diagram이다.
원래는 이차함수의 모양을 가졌지만, 주기적인 배열의 원자핵과 그로 인한 potential로 인해 같은 모양의 곡선이 일정 주기로 반복된다. bloch function이라고 주기 a마다 곡선이 반복되는 함수를 의미한다. 고체의 lattice parameter(원자의 배열 주기)가 a일 때 k space에서 이 주기는 2π/a(2π/L)가 된다.
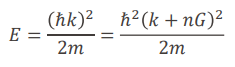
이 과정에서 곡선이 끊기는 곳이 생긴다. 위 그래프에서 보니 원자핵과 원자핵 사이에 끊기는 곳이 생긴다. 전자는 +전하를 띈 원자핵에 가까이 있고 싶어 한다. 저렇게 원자핵과 원자핵 중간에 있는 곳은 전자가 선호하는 곳이 아니다. 즉, 저 구간에는 전자가 존재하지 않는다. 그래서 끊겨있다. 그래서 전자가 존재하지 않는 에너지 구간이 생기는데 이를 forbidden band라고 한다. 실제 고체 물질들은 많은 원자가 주기적으로 배열되어 있기 때문에 이러한 periodic potential 모델처럼 끊기는 구간이 있다. 이를 band gap이라 한다. 즉, 전자가 존재하지 않는 구역을 band gap이라고 생각하면 된다.
위 그래프는 정말 periodic potential을 간단하게 표현한 거고 실제 물질들의 band structure은 조금 더 복잡하다.
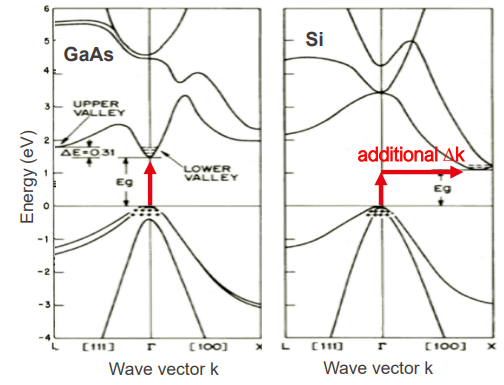
진짜 복잡하게 생겼다. 그 이유는 고체 원자가 주기적으로 배열되어 있더라도 바라보는 방향에 따라 주기나 퍼텐셜이 달라지기 때문이다.
아무튼 윗 그림에서 왼쪽처럼 conduction band의 최저점과 valence band의 최고점의 k-position이 일치하는 경우를 direct bandgap, 오른쪽처럼 일치하지 않으면 indirect bandgap이라 한다. Direct bandgap은 에너지만 얻으면 k값을 바꾸지 않아도 전자가 conduction band로 전이할 수 있기 때문에 absorption이 강하다. (GaAs의 사례) 반면, indirect bandgap은 에너지도 얻어야 하고, k값도 바꿔야하기 때문에 복잡하다. 따라서 전자가 CB로 전이하기 어렵다. (Si의 사례) 위 곡선의 curvature를 통해 carrier의 effective mass를 알 수 있다. effective mass는 curvature에 반비례한다.
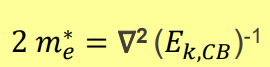
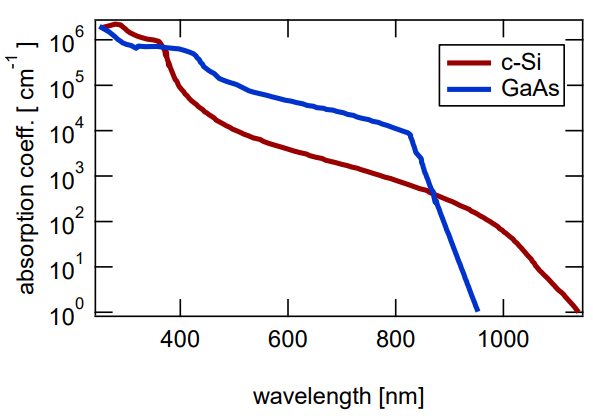
GaAs(Direct)와 Si(Indirect)의 absorption coefficient를 비교했다. visible light영역에서 GaAs의 흡광이 훨씬 잘 일어난다. 그 이유는 GaAs가 direct bandgap이기 때문이다. 때문에 Si는 빛을 잘 흡수하지 않기 때문에 두꺼워야 한다. 반면, GaAs는 빛을 잘 흡수하기 때문에 thin film으로 만들어도 된다. 그래서 Si wafer는 얇게 만들 수 없다. 하지만 Si이 훨씬 싸기 때문에 여전히 Si wafer를 많이 쓴다.
위의 복잡한 band structure를 간단히 표현하면 아래와 같다. valence band는 전자가 차있는 아래 밴드, conduction band는 전자가 차있지 않은 윗부분, 그리고 그 사이 전자가 존재할 수 없는 band gap.
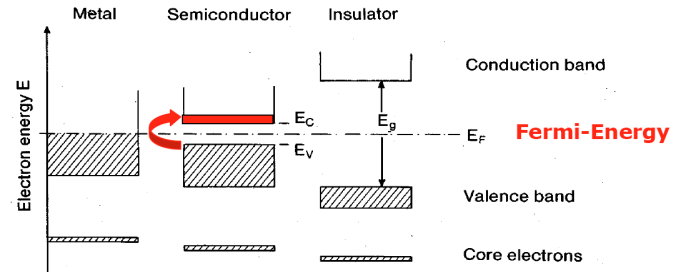
금속은 valence band와 conduction band 사이에 band gap이 없다. 그래서 전자가 바로 전이할 수 있어 전기전도도가 매우 좋다. 반도체는 VB와 CB사이에 작은 갭이 있다. 그래서 전자가 약간의 에너지를 얻어서 CB로 전이해야 전기전도도가 생긴다. 부도체는 밴드갭이 너무 커서 많은 에너지를 줘도 전이하지 않는다. 따라서, 전기전도도가 거의 없다.
Fermi energy라는 새로운 개념이 보인다. fermi energy는 상황에 따라 정의가 달라진다. T=0K에서, 페르미 준위는 전자가 채워질 수 있는 가장 높은 에너지, T>0K에서 페르미 준위는 전자의 발견 확률이 50%인 에너지이다. 왜 헷갈리게 둘이 정의가 다르지?라고 생각할 수 있겠지만, 결과적으로 같다는 걸 알게 될 것이다.
'태양전지 교과서' 카테고리의 다른 글
| [태양전지 교과서] Week 5 - Extrinsic semiconductors (0) | 2025.01.25 |
|---|---|
| [태양전지 교과서] Week 5 - Fermi level & Fermi-Dirac distribution (0) | 2025.01.25 |
| [태양전지 교과서] Week 4 - Sustainability (0) | 2025.01.25 |
| [태양전지 교과서] Week 3 - PV Application (0) | 2025.01.25 |
| [태양전지 교과서] Week 3 - Connecting PV to outside (0) | 2025.01.25 |





